Purpose
In this multi-part blog post, we try to understand
Why do we need stereo-computer vision?
Given any stereo cameras, how can we calibrate and use them to find depth?
Why do we need Stereo?
TL;DR
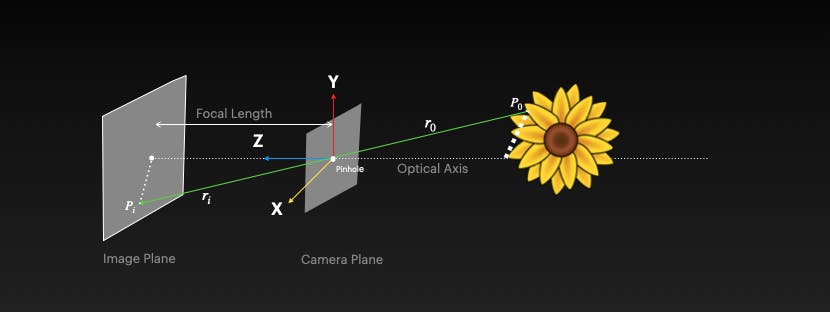
When we take a picture of an object, we lose the "depth" information
To regain the "depth", we need another camera pointing at the same object, that will provide the necessary parameters to mathematically derive such information.
The loss of depth
Given a point in the image (U, V), can we find a corresponding point in the world? When we capture an image, the 3D world coordinates get transformed into camera coordinates and then into a 2D image. Given an image point, you cannot reverse engineer to get world coordinates since you have lost a crucial "Z" coordinate in the translation process. However, you haven't lost "X" and "Y". There is hope to get them back, but we need additional help.
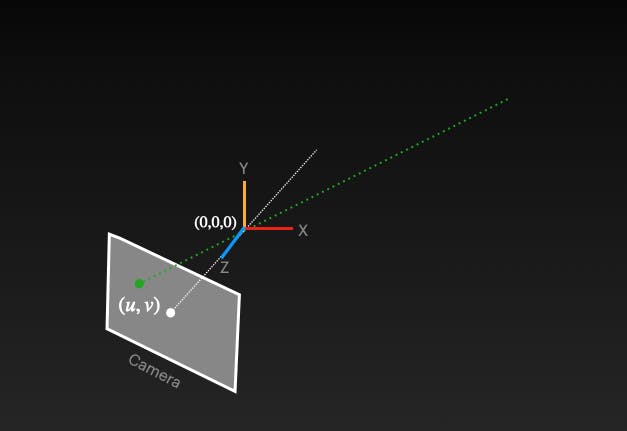
Since we know "X" and "Y", we know it exists somewhere along the line shown as dotted green lines. Why? This was the same line that is used in the projection of an object onto the image plane. So, it can also assist in the reverse direction as well.
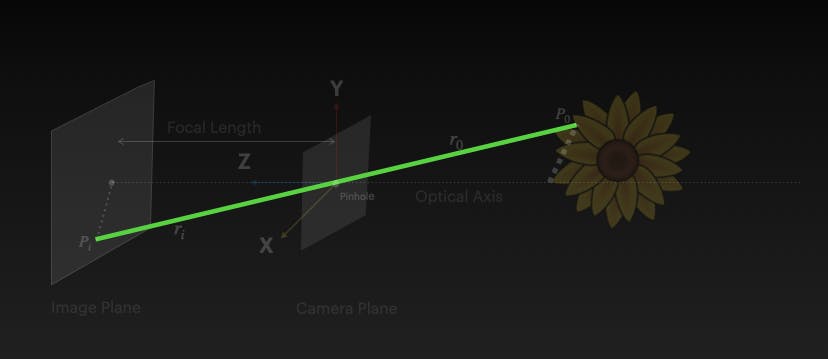
How to recover?
The trick is to understand how nature does this. We all have 2 eyes, and we perceive depth (3D) in all objects. Don't we? The "second eye" provides its view of the world in addition to the first, and both together work to perceive depth.
Let's apply the same concept here. let's bring in another camera, place it horizontally along the same axis at a distance, find the same spot (U, V) on it, and project the point on the "dotted green line". The intersection of these 2 dotted green lines gives you the depth Z. See below for the visual
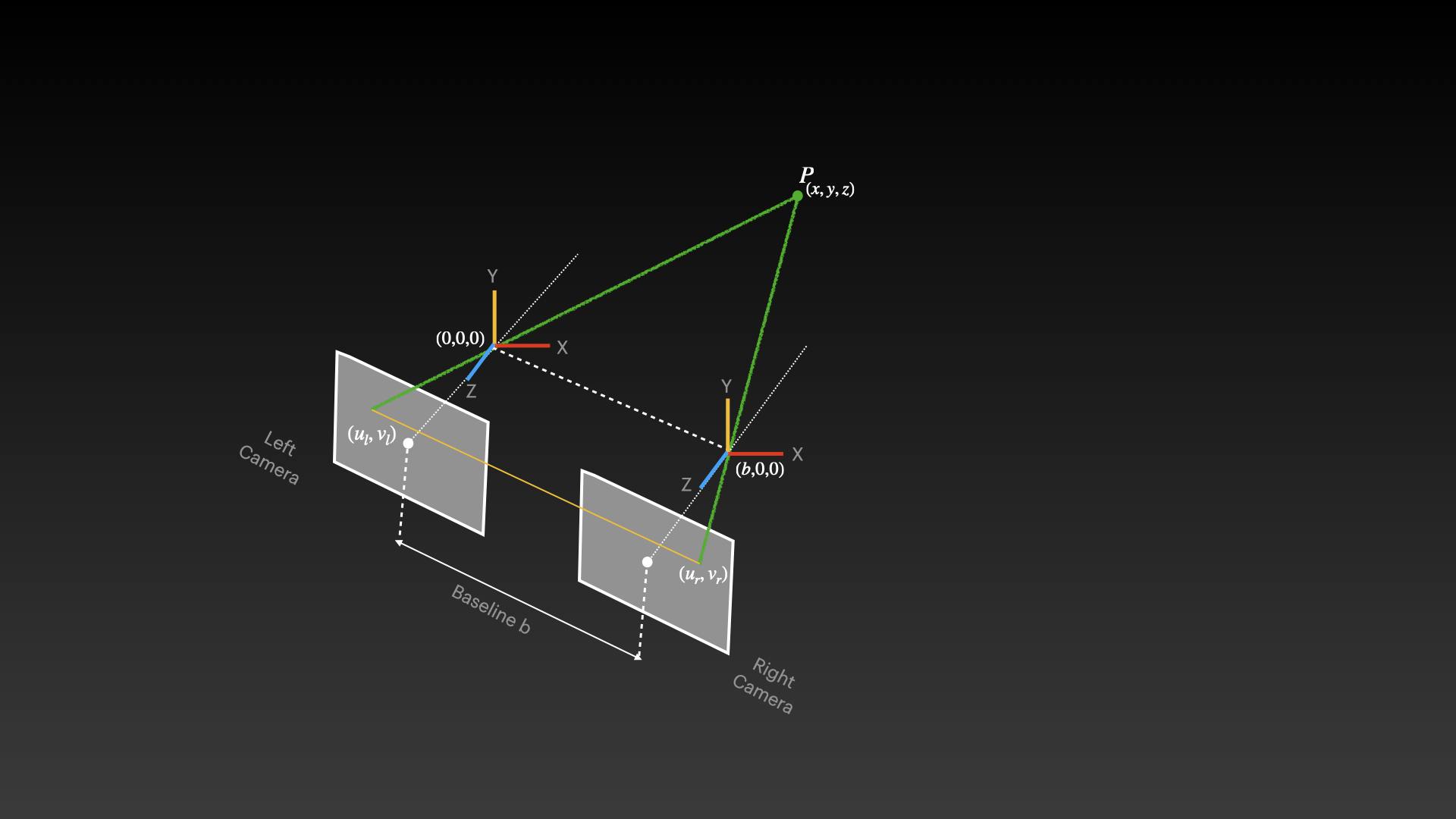
\( u_r v_r \) and \( u_l v_l \) are the same points of the image as seen in the right and left camera respectively
the distance between the cameras is called BASELINE denoted by b
the camera plane is placed at the pinhole with origin (0,0,0) on the left and (b,0,0) on the right
P (x, y, z) is the scene point that we are trying to compute using the 2 cameras.
This concept of using 2 cameras to perceive depth in the real world is Stereo Vision.
Finding Depth
Let's start with the basics. For a pinhole-based camera system, we know the following equations.
\(u_l = f_x * x/z + O_x\)
\(v_l = f_y * y/z + O_y\)
\(f_x, f_y\) are the x and y coordinates of the focal point of the camera. \(O_x O_y\)are the offsets from the center of the image sensor.
For the right camera, its the same but the camera X axis is shifted by "b"
\(u_r = f_x * (x-b)/z + O_x\)
\( v_r = f_y * y/z + O_y \)
Using the 4 equations, solving for X, Y, and Z we get
\(X = \frac {b (u_l - O_x)}{ u_l - u_r }\)
\(Y = \frac {b f_x (v_l - O_y)}{f_y (u_l - u_r)}\)
\(Z = \frac {b f_x}{ u_l - u_r }\)
\( u_l - u_r \) is called DISPARITY and it's inversely proportional to "Z". If the object is closer to the camera, you will see a large disparity.
The disparity is proportional to the baseline i.e. if the distance between camera increase, the disparity will increase.
So, if we know the internal parameters of the camera i.e. \(f_x, f_y, O_x, O_y\) and hence compute disparity, we can calculate Z (depth)!
Few Thoughts on Disparity
Note that there is no (\(v_l - v_r \) ) in the equation, which means only the horizontal component between the two cameras varies and not the "vertical component". This means points (\(u_r, v_r\)) and ( \( u_l \) \( v_l \) ) lie along the same line (shown by the yellow line).
So, when we are calculating DISPARITY to solve for X, Y and Z, we can pick a point in the left camera \( (u_l, v_l) \) and ONLY search along the same line in the right camera (and avoid searching the whole image) to get the \( u_r, v_r \) .i.e it's a 1-dimensional (1D) search problem. See the image below for an example. This is often called the "correspondence problem"

The white patch in the picture is called the "scan line".
Problems with stereo matching
Did we solve finding depth just by solving 2 cameras? Yes, for the most part, but if the images have a repetitive texture, it's impossible to compute disparity and therefore can't compute depth. see the image below.

Next Steps
In the next part, we will understand how to calibrate stereo cameras and use them to compute depth

